很多人觉得排列组合公式很难，小编把这些例子公式发上来与大家分享，希望能帮助到你。

排列及计算公式

01、从n个不同元素中，任取m(m≤n)个元素按照一定的顺序排成一列，叫做从n个不同元素中取出m个元素的一个排列;从n个不同元素中取出m(m≤n)个元素的所有排列的个数，叫做从n个不同元素中取出m个元素的排列数，用符号 p(n,m)表示.
p(n,m)=n(n-1)(n-2)……(n-m+1)= n!/(n-m)!(规定0!=1)。

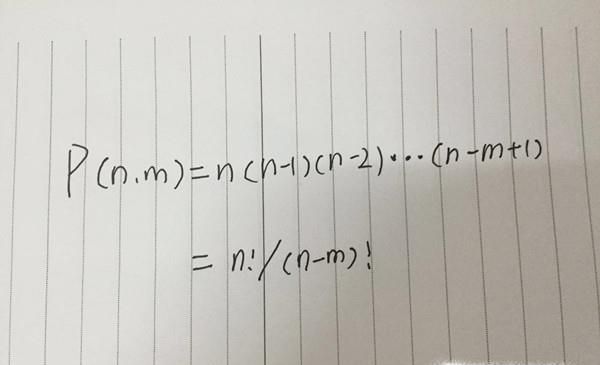
02、用具体的例子来理解上面的定义：4种颜色按不同颜色，进行排列，有多少种排列方法，如果是6种颜色呢。从6种颜色中取出4种进行排列呢。
解：A(4,4)=4x(4-1)x(4-2)x(4-3)x(4-4+1)=4x1x2x3x1=24。
A(6,6)=6x5x4x3x2x1=720。
A(6,4)=6!/(6-4)!=(6x5x4x3x2x1)/2=360。

组合及计算公式

01、从n个不同元素中，任取m(m≤n)个元素并成一组，叫做从n个不同元素中取出m个元素的一个组合;从n个不同元素中取出m(m≤n)个元素的所有组合的个数，叫做从n个不同元素中取出m个元素的组合数.用符号c(n,m) 表示.
c(n,m)=p(n,m)/m!=n!/((n-m)!*m!);c(n,m)=c(n,n-m)。

02、用具体的例子来理解上面的定义：6!=6x5x4x3x2x1=720，4!=4x3x2x1=24。

其他排列与组合公式

01、从n个元素中取出r个元素的循环排列数=p(n,r)/r=n!/r(n-r)。
n个元素被分成k类，每类的个数分别是n1,n2,...nk这n个元素的全排列数为
n!/(n1!*n2!*...*nk!)。
k类元素,每类的个数无限,从中取出m个元素的组合数为c(m+k-1,m)。

02、用例子来理解定义：从4种颜色中，取出2种颜色，能形成多少种组合。
解：C(4,2)=A(4,2)/2!={[4x(4-1)x(4-2)x(4-3)x(4-4+1)]/[2x(2-1)x(2-2+1)]}/[2x(2-1)x(2-2+1)]=[(4x3x2x1)/2]/2=6。

排列Pnm

01、排列(Pnm(n为下标，m为上标))。
Pnm=n×(n-1)....(n-m+1);Pnm=n!/(n-m)!(注：!是阶乘符号);Pnn(两个n分别为上标和下标) =n!;0!=1;Pn1(n为下标1为上标)=n
组合(Cnm(n为下标，m为上标))
Cnm=Pnm/Pmm ;Cnm=n!/m!(n-m)!;Cnn(两个n分别为上标和下标) =1 ;Cn1(n为下标1为上标)=n;Cnm=Cnn-m
公式P是指排列，从N个元素取R个进行排列。公式C是指组合，从N个元素取R个，不进行排列。N-元素的总个数 R参与选择的元素个数 !-阶乘。
如  ：9!=9*8*7*6*5*4*3*2*1
从N倒数r个，表达式应该为n*(n-1)*(n-2)..(n-r+1);因为从n到(n-r+1)个数为n-(n-r+1)=r